Implementing a liquidity pool with Python

Rebeca Sarai · September 3, 2022

crypto web3 python

Introduction
Constant Product Automated Market Maker
Liquidity providers
Risks
Starting to code
Creating a pool
Adding liquidity to the pool
Swapping tokens
Conclusion
Links

In this post, I will implement a liquidity pool using python and regular data structures, with no blockchain, and no contract code. The intention is to get a better understanding on how liquidity pools work economically, without diving in blockchain development details.

Introduction

Liquidity pools are an essential part of Defi because they enable users to exchange tokens without the need of a trusted mediator, as is the case with centralized exchanges such as Coinbase.

This mechanism can be understood as a black box that enables unstoppable and automated trading based on prices defines by an algorithm.

Unstoppable because once the mechanism is live, one should not be able to modify the implementation or even stop the mechanism. The only way to disable it is for users to stop using it.
Automated because the pricing of the assets is not dependent of users wanting to buy/sell, instead prices are defined algorithmically.

Algorithms used to manage liquidity pools are called Automated Market Makers (AMM) and the simplest one is called: Constant Product Automated Market Maker.

Constant Product Automated Market Maker

Liquidity pools aid in avoiding large price swings by using algorithms to regulate the trade price.

The constant product formula is described below, and its result must remain constant despite the size of the trade, meaning that the total amount of liquidity on the pool remains constant:

X * Y = K
X represents the number of tokens of type X
Y represents the number of tokens of type Y
K is the multiplication of the amount of both tokens and must remain constant

This results in a seesaw effect, when the value of one token increases, the value of the other decreases, and vice versa. The formula dictates each transaction’s price, regardless of how much of either token is bought or sold at any given point.

Two details are extremely important to understand here:

Smaller markets are subjected to high price variations on transactions since there’s not enough weight on the market, every transaction can impact the seesaw. So the more liquidity there is in a pool, the smaller impact trades will have on the value of the assets within that pool.
Since the value of assets is determined algorithmically, the system depends on the arbitrage of other actors to keep the current market price. Ex: buying items from the pool at a “discount” price and re-selling it at a secondary market for a profit.

Liquidity providers

As mentioned in the previous topic, smaller markets are subject to high price fluctuations due to the algorithmic nature of the pools. Liquidity providers are rewarded with transaction fees for allowing other traders to buy and sell using your liquidity. However, this is not a risk-free investment, one also needs to account for impermanent loss, which takes place when a trader places their tokens within a liquidity pool and then the price changes. The value of those tokens is now less than it was at the time of the investment, which means if you remove them now, their value will have decreased.

These losses are called impermanent because until you remove the investment from the liquidity pool, the loss is not materialized. You can wait to remove your liquidity until the exchange reaches a favorable point (but this can never come to fruition).

Risks

Other than the risk for liquidity providers described in the previous section, there is also systemic risks of interacting with these mechanisms.

These markets are self-sustaining because they don’t need intermediaries. Formulas power smart contracts that provide security and confidence for investors. However, you need to verify in order to gain confidence in the project you are using, contracts can have bugs, founders can be ill-intentioned (e.g. create backdoors on their project to remove profits), and the ecosystem around the protocol can collapse (e.g.: Terra disaster), and etc.

Starting to code

We want to enable the following functionalities:

Trade one token for another freely
Add liquidity to the pool
Remove their share of liquidity of the pool

Some general notes on how we want to approach this implementation:

One liquidity pool should have two tokens
The pricing algorithm will be the Constant Product
All operations must keep the K value constant
The token ratio determines the pool’s pricing. For example, when someone buys DAI from the DAI/ETH pool, the volume of ETH increases, raising the price of DAI while lowering the price of ETH.
But the total price adjustment will depend on how much the person spent and how much the pool was altered.
For simplicity, we will not consider transaction fees.
Price is determined by: price_token_A = reserve_token_B / reserve_token_A (Y / X)

Creating a pool

Liquidity pools will be called Exchange and as mentioned previously the implementation will be made in Python.

class Exchange:
    """
        Exchanges is how uniswap calls the liquidity pools
    """

    def __init__(self, token0_name: str, token1_name: str, name: str, symbol: str) -> None:
        self.token0 = token0_name
        self.token1 = token1_name
        self.reserve0 = 0
        self.reserve1 = 0
        self.fee = 0

        self.name = name
        self.symbol = symbol
        self.liquidity_providers = {}
        self.total_supply = 0

All the storage needed is reserve0 and reserve1, to hold the number of tokens of each asset. Other attributes are secondary and are used to ease implementation and keep a record of what’s happening in the pool.

Adding liquidity to the pool

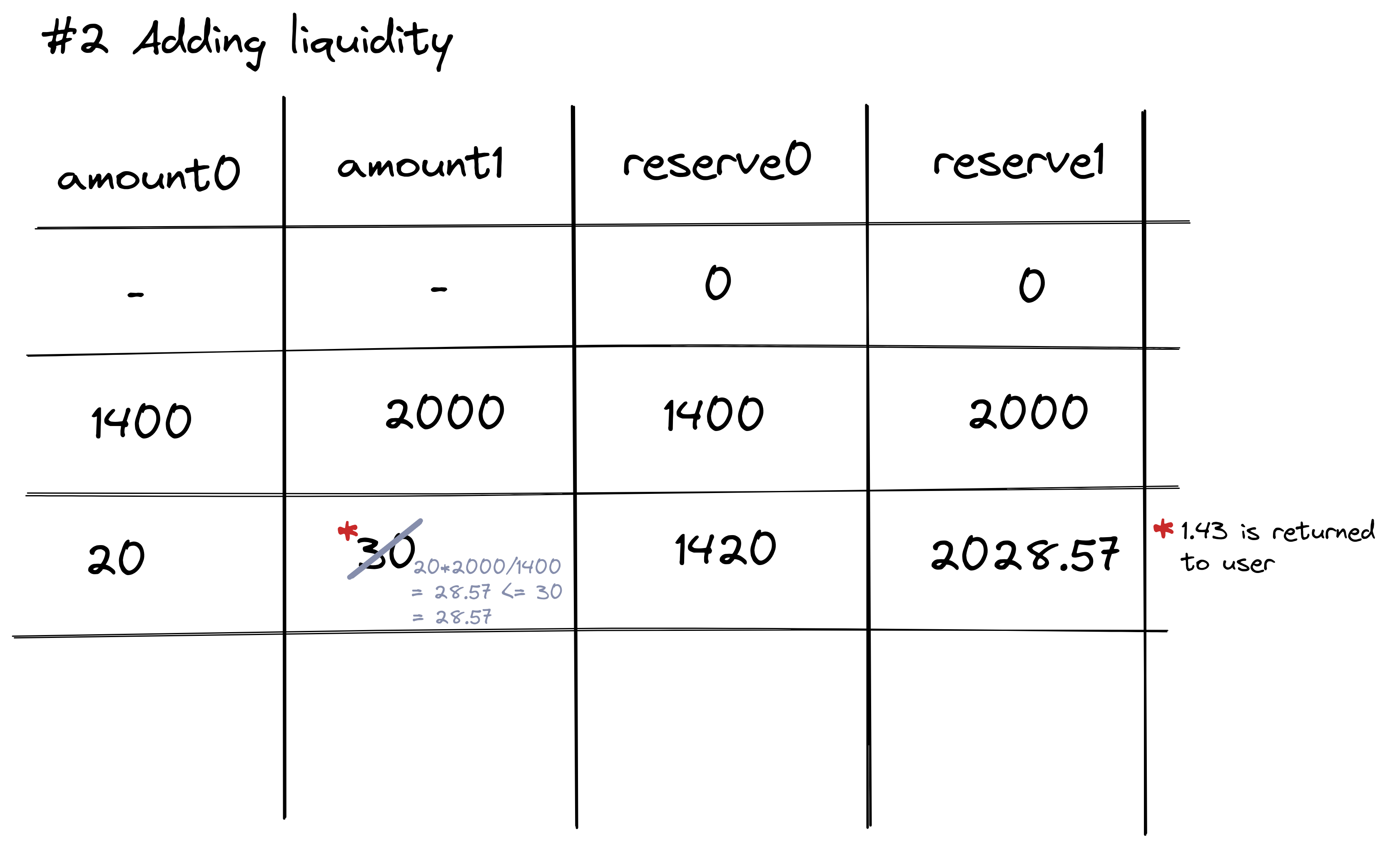
Adding liquidity means updating the reserves to enable trading. When adding liquidity to a pool for the first time, the pool’s creator determines each asset’s initial price. However, if the pool’s pricing does not match that of the global crypto market, the liquidity provider risks losing money.

After the first time, the liquidity added to both pairs must match a minimal value, which is defined by (amount0 * reserve1) / reserve0.

class Exchange

    # ...

    def quote(self, amount0, reserve0, reserve1):
        """
        Given some amount of an asset and pair reserves, returns an equivalent amount of
        the other asset
        """
        assert amount0 > 0, 'UniswapV2Library: INSUFFICIENT_AMOUNT'
        assert reserve0 > 0 and reserve1 > 0, 'UniswapV2Library: INSUFFICIENT_LIQUIDITY'
        return (amount0 * reserve1) / reserve0;

    def _add_liquidity(self, balance0, balance1):
        """
        You always need to add liquidity to both types of coins
        """
        if self.reserve0 == 0 and self.reserve1 == 0:
            # initializing pool
            amount0 = balance0
            amount1 = balance1
        else:
            balance1Optimal = self.quote(balance0, self.reserve0, self.reserve1)
            if balance1Optimal <= balance1:
                amount0 = balance0
                amount1 = balance1Optimal
            else:
                balance0Optimal = self.quote(balance1, self.reserve1, self.reserve0)
                assert balance0Optimal <= balance0
                amount0 = balance0Optimal
                amount1 = balance1

        self.reserve0 += amount0
        self.reserve1 += amount1

A visual example is the image below, the algorithm will force the user to always add the same amount of liquidity to both assets in the pool.

Table with amount0, amount1, reserve0, reserve1

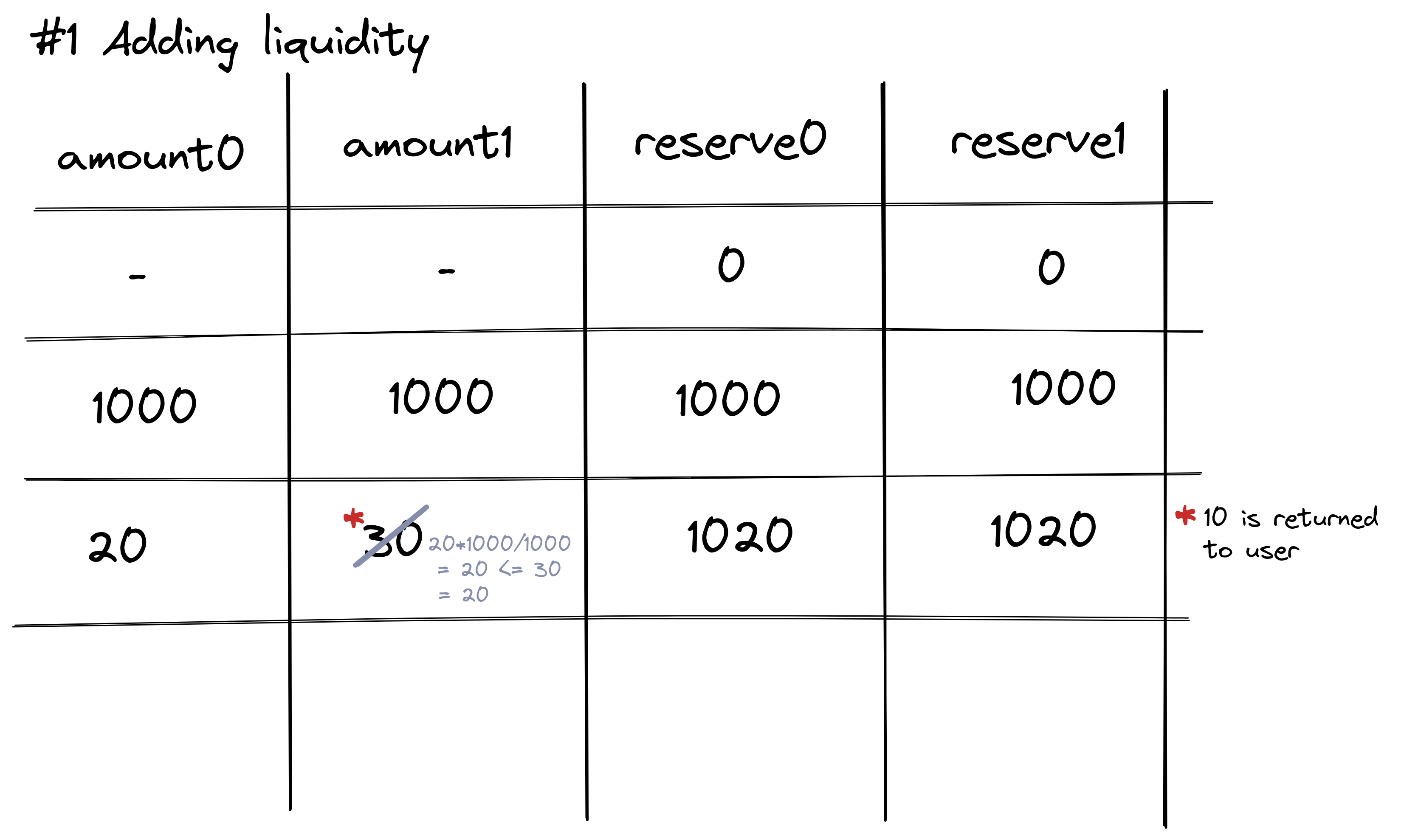
This is extremely important when the pool is unbalanced, due to trades and negotiations that make the pool price equal to the market price.

Table with amount0, amount1, reserve0, reserve1

Swapping tokens

The implementation to swap tokens has more assertions than the actual code. The magic happens in the get_amount_out function, which calculates the correct amount out given the reserves of the pool.

class Exchange
    # ...

    def get_amount_out(self, amount_in):
        """
        Given an input amount of an asset and pair reserves, returns the maximum output amount of the
        other asset

        (reserve0 + amount_in_with_fee) * (reserve1 - amount_out) = reserve1 * reserve0
        """
        assert amount_in > 0, 'UniswapV2Library: INSUFFICIENT_INPUT_AMOUNT'
        assert self.reserve0 > 0 and self.reserve1 > 0, 'UniswapV2Library: INSUFFICIENT_LIQUIDITY'

        amount_in_with_fee = amount_in * 1000              # disconsidering the fee here: amount_in * 997
        numerator = amount_in_with_fee * self.reserve1
        denominator = self.reserve0 * 1000 + amount_in_with_fee
        amount_out = numerator / denominator

        return amount_out


    def swapExactTokensForTokens(self, amount0_in, amount1_out_min):
        amount0_out = 0
        amount1_out = self.get_amount_out(amount0_in)
        assert amount1_out >= amount1_out_min, 'UniswapV2Router: INSUFFICIENT_OUTPUT_AMOUNT'

        assert amount1_out > 0, 'UniswapV2: INSUFFICIENT_OUTPUT_AMOUNT'
        assert amount0_out < self.reserve0 and amount1_out < self.reserve1, 'UniswapV2: INSUFFICIENT_LIQUIDITY'

        balance0 = self.reserve0 + amount0_in - amount0_out
        balance1 = self.reverve1 - amount1_out
        balance0_adjusted = balance0 * 1000
        balance1_adjusted = balance1 * 1000
        assert balance0_adjusted * balance1_adjusted == self.reserve0 * self.reserve1 * 1000**2, 'UniswapV2: K'

        self.reserve0 = balance0
        self.reserve1 = balance1

        return amount1_out

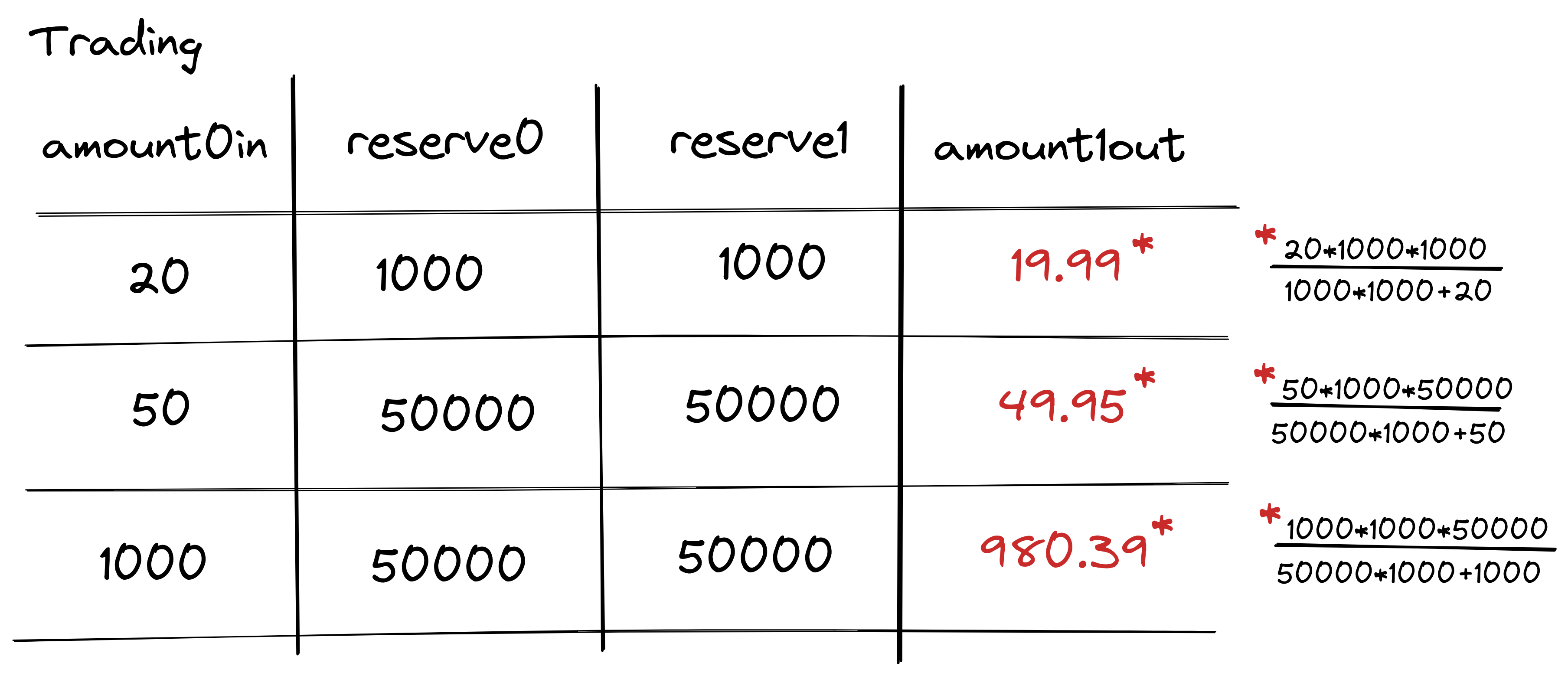
Below is a set of example transactions, note that the difference between the amount in and the amount out increases as the transaction amount increases. This is what was described as the seesaw effect.

Table showing the amount out depending on the amount in and reserves

Conclusion

In this post, you just saw how to implement a liquidity pool using python and regular data structures, no blockchain, no contract code. A more complex implementation replicating the architecture used on smart contracts can be found here.

Links

Did I make a mistake? Please consider sending a pull request.